Although the 3d quad method implemented in xflr5 performs well and is both robust and resilient, it suffers from two drawbacks which have been explained in the xflr5 theoretical documents. Firstly, general 3d surfaces cannot be covered by flat quadrilateral elements. Secondly, the method is of the uniform type, which may be inadequate for modelling areas of sharp pressure gradients.
Furthermore, surfaces resulting from the intersection of the fuselage and wings can only be meshed properly using triangles, and therefore require a method based on triangular panels.
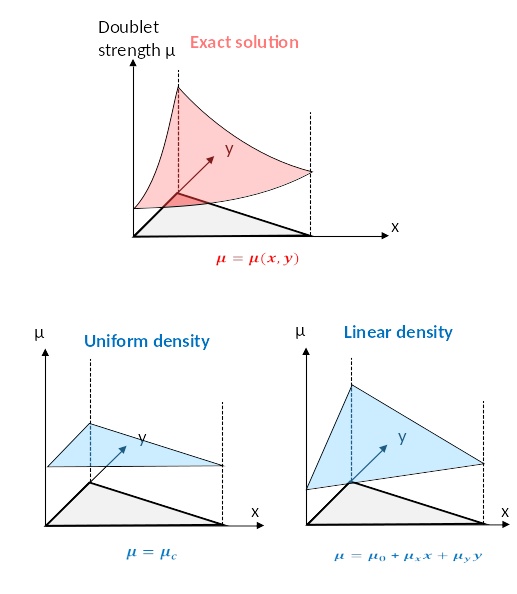
These issues are resolved with Galerkin-type triangular formulations. Two such methods have been implemented in flow5, one with uniform sources and doublet distributions and the other with uniform sources and linear doublets. They can be used with either thin or thick wing representations.
Preliminary testing has shown that all three methods, i.e. quads, uniform triangles and linear triangles, lead to comparable results for simple configurations. Differences are more notable with complex geometries, for instance when the configuration includes fuselage-wing intersections, winglets or flap deflections.
The linear method is more precise in theory but uses 3 degrees of freedom for each mesh element, which leads to matrix sizes three times the size of matrices generated by uniform methods. It is worth noting that the memory usage increases as n², and the time to solve the linear system increases as 2/3 n³. Testing has shown that an 8 GB RAM computer can handle matrix sizes up to 15kx15x. The latter point is not an issue either, because the Intel MKL library and the use of multi-threading have dramatically reduced analysis times compared to xflr5.
The recommended method is the linear triangular formulation, or the triangular uniform method for reduced analysis times in the preliminary design stages.
References
The key building block of a Galerkin method is the evaluation of singular and hyper-singular surface integrals on triangles.
flow5 implements
– for in-plane integrals: the methods proposed Michael J. Carley, in “Analytical Formulae for Potential Integrals on Triangles.” Journal of Applied Mechanics 80.4 (2013).
– for off-plane integrals the method proposed by Sylvain Nintcheu-Fata in Explicit expressions for 3D boundary integrals in potential theory, Int. J. Numer. Meth. Engng 2009; 78:32–47
The first method has the advantage of simplicity, but becomes unstable when the field point is close to, but not on, the triangle’s plane.
The second method is more robust, however the integral is undefined when the projection of the field point is on the triangle’s edge.
