Ground and free surface effects

Updated December 17th, 2021

------------------ WORK IN PROGRESS ------------------

Theory

Back to main table of contents

From the physical point of view, the ground or water surface is a horizontal plane such that the normal component of the velocity on this plane is zero. The viscous layer on the ground surface is ignored so that there is no constraint on the tangential velocity. In the case of the sail analyses there is the option in flow5 to define a wind gradient, but this is set as an input parameter and is not a result of the analysis.
Rather than to introduce an additional surface in the analysis to simulate the ground, it is usual and simpler in potential methods to add in the analysis the contribution of a virtual mirror model opposite the ground surface. This circulation of doublet strengths of the virtual model have the opposite sign as those of the bound vortex. By symmetry, this ensures that the boundary condition Vz=0 is satisfied on the ground surface.
This is the way that ground or water surfaces are included in flow5 both for plane and sail analyses.

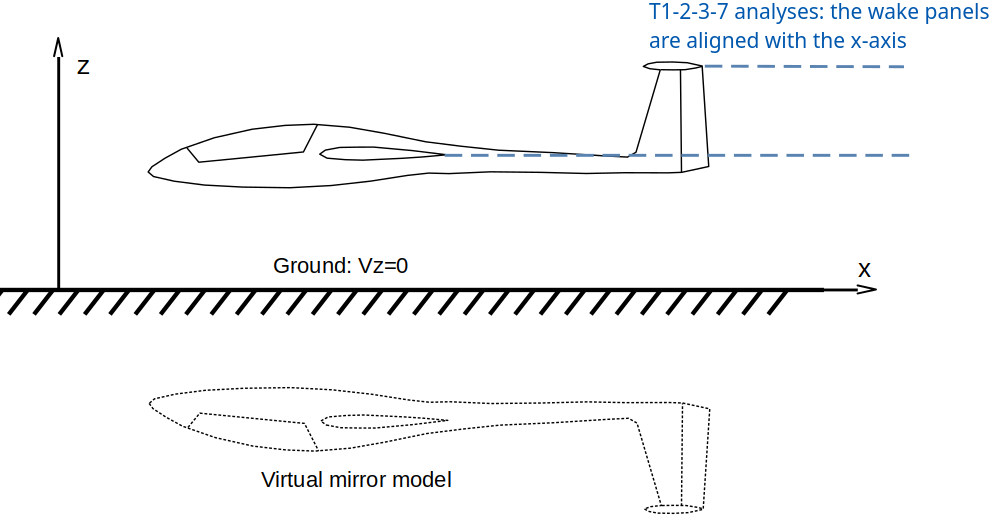
Due to the proximity of the model to the surface, the way in which the surface elements and the wake elements are defined may influence the results.
In the case of the linear T1-2-3-5-7-8 analyses, the mesh is not rotated with the a.o.a. and the wake panels are aligned with the x-axis whatever the angle of attack, as illustrated in the figure above.

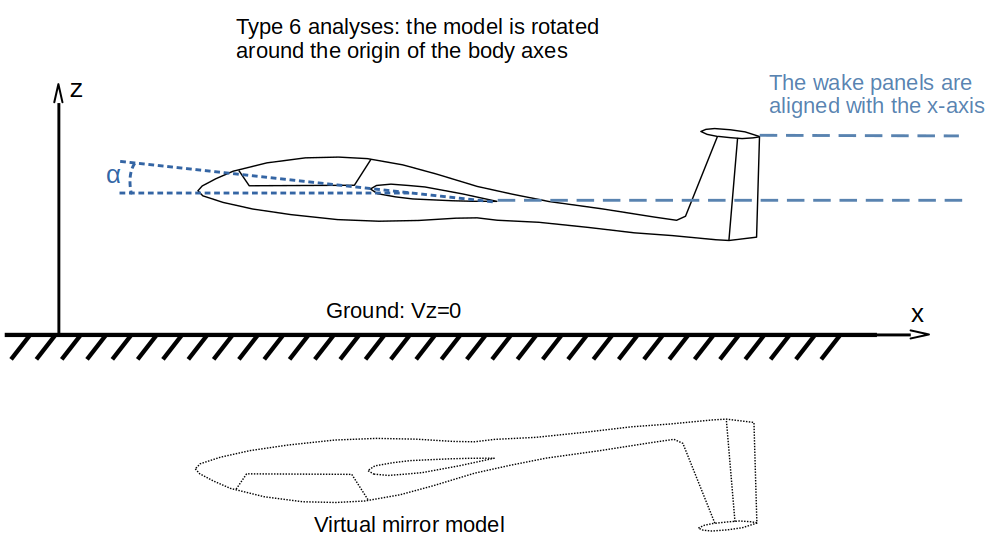
In the case of T6 analyses, the calculation is performed in stability axes, i.e. the model is rotated by the angle of attack α around the y-axis of the body frame as illustrated in the figure below. The flat wake panels are aligned with the x-axis whatever the angle of attack. In the case of plane analyses, this is more representative of the physical problem. The recommended way however is to use a vortex particle wake, where the vortons will follow the streamlines and adapt to the presence of the ground surface.

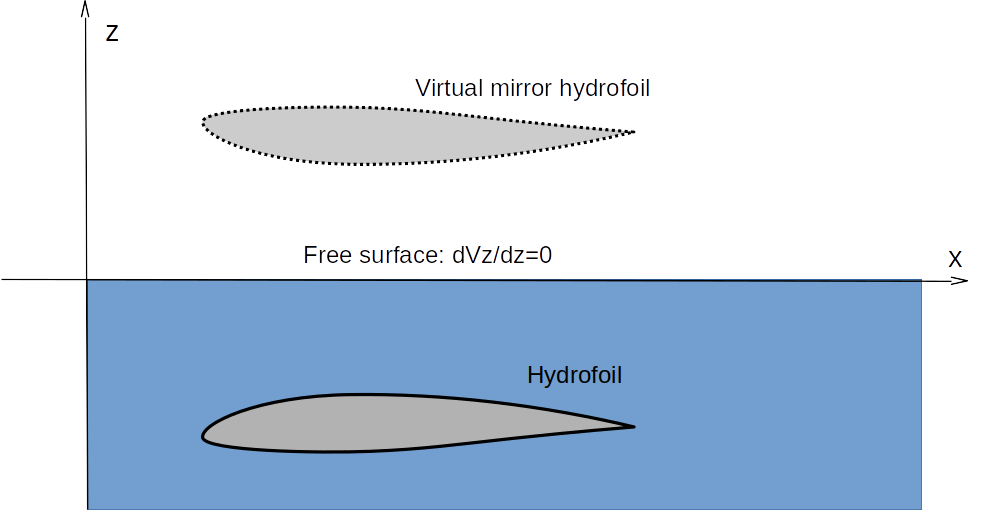
Free surface effect

The free surface effect is implemented in flow5 in accordance with the method described in NASA Report 1232 "A THEORETICAL AND EXPERIMENTAL INVESTIGATION OF THE LIFT AND DRAG CHARACTERISTICS OF HYDROFOILS AT SUBCRITICAL AND SUPERCRITICAL SPEEDS", By KENNETH L. WAD LIN, CHARLES L. SHUFORD, Jr., and JOHN R. McGEHEE, 1955.

The free surface is such that the normal pressure on this surface is zero. This is equivalent to having a zero slope of the velocity component normal to this surface. To force this condition, the method is essentially the same as for the ground effect, except that the circulation of doublet strengths of the virtual model are the same as those of the real model.

An infinite Froude number is assumed.

Implementation in flow5

Ground effect

The ground effect is activated in the analysis definition, and a height to ground is specified. This height should be positive. It is the distance of the origin of the body axes to the ground.

From the numerical point of view, no mesh elements for the virtual mirror model are added in the analysis. This would increase unnecessarily the matrix size and the analysis times. Instead, each time that the contribution of a panel to the potential function or to the velocity vector is required in the analysis, the contribution of the symmetric panel is added. This implies that the construction times of the influence matrix and the RHS are slightly increased, but that the matrix size remains unchanged.

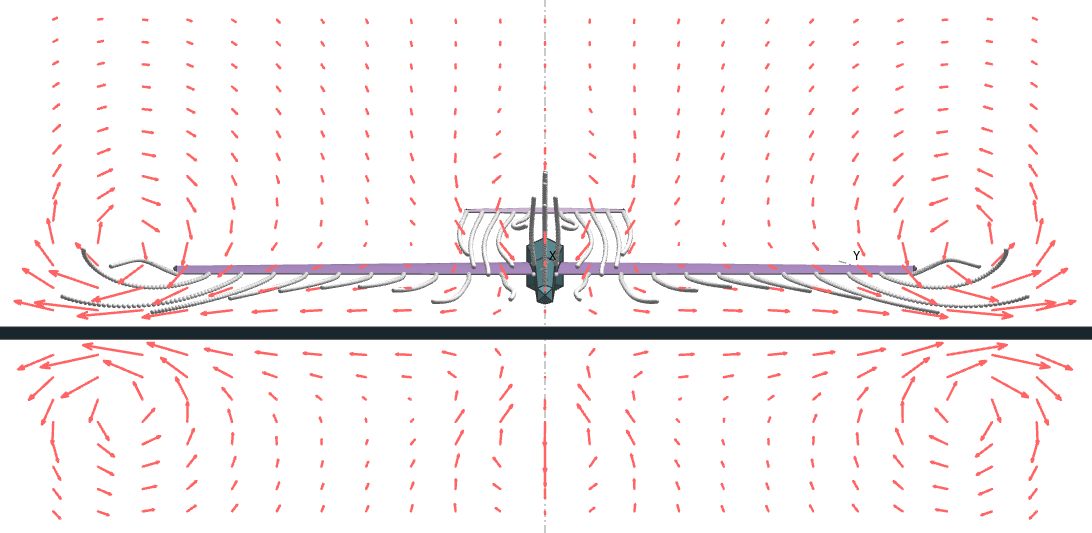
As a sanity check, the ground and water surfaces can be displayed respectively for plane and sailboat analyses.
The crossflow velocities can also by displayed and will confirm that the vectors are tangent to the ground surface as illustrated in the figures below.

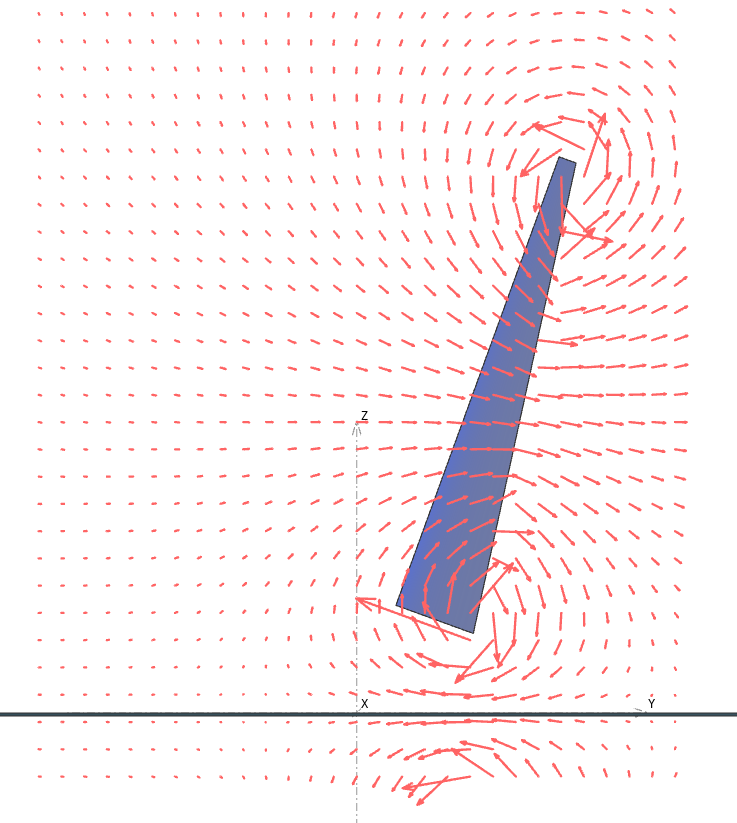
The inclusion of the ground effect reduces the induced drag and increases the lift. Cf. the red curve in the graph below.

Free surface

The free surface effect is activated in the analysis definition, and a height to the free surface is specified. This height should be negative. It is the distance of the origin of the body axes to the free surface.

From the numerical point of view, the implementation is common to that of the ground effect except for the sign of the circulations or doublet strenghts which are identical to those of the model instead of being opposite.

The display of the free surface and of the crossflow velocities can by displayed in the 3d view to confirm that the analysis is defined as intended.

The test cases of NASA report 1232 have been modelled in flow5. The results are presented here.

Conclusions and recommendations

The visual sanity checks are a good indicator that the ground and free surface effects are implemented in flow5 in conformity with the theoretical model.

in the case of the ground effect, the lift and drag tend to improve significantly compared to the case of the infinitely distant ground surface, which is what is expected. There is unfortunately no publicly available experimental data to use to benchmark flow5 results.
Given the proximity to the surface, the calculation in stability axes used in T6 polars is expected to be more representative and is the recommended way.
Lastly the VPW should be preferred to the flat panel wake model for its greater numerical robustness perticularly for the calculation of moments.