Contents

The following results were obtained after improvement of the triangular linear method in V7.01 beta 09.

• Sphere
• Cylinder
• Conclusion and recommendation

Back to table of contents

---

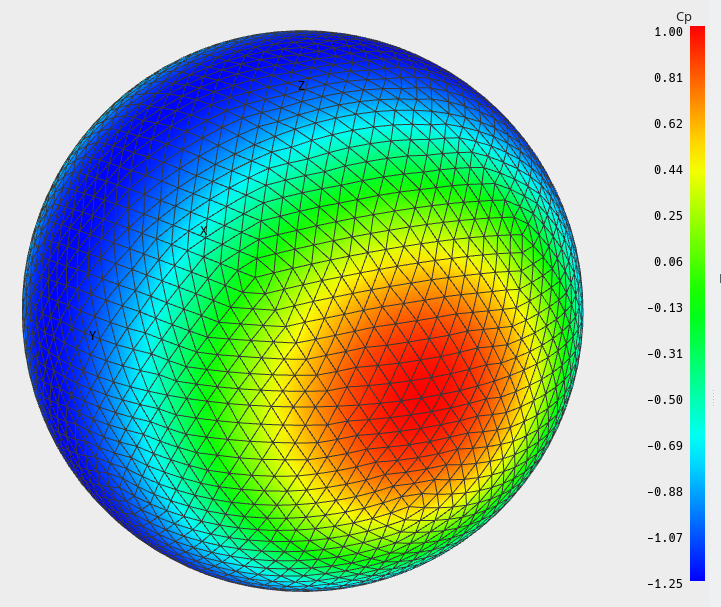
Sphere

The pressure coefficient on the surface of a sphere in the plane of symmetry is Cp = 1 - 9/4 sin²(θ)
where the origin of the angle θ is taken at the leading point.
The pressure coefficients are therefore:

Cp=1 at the leading point.
Cp=-1.25 at the top point.

The error decreases with the number of surface elements: It can be noted that the linear method is more precise, but that the uniform methods catches up in precision for mesh sizes greater than 1000.

Back to top

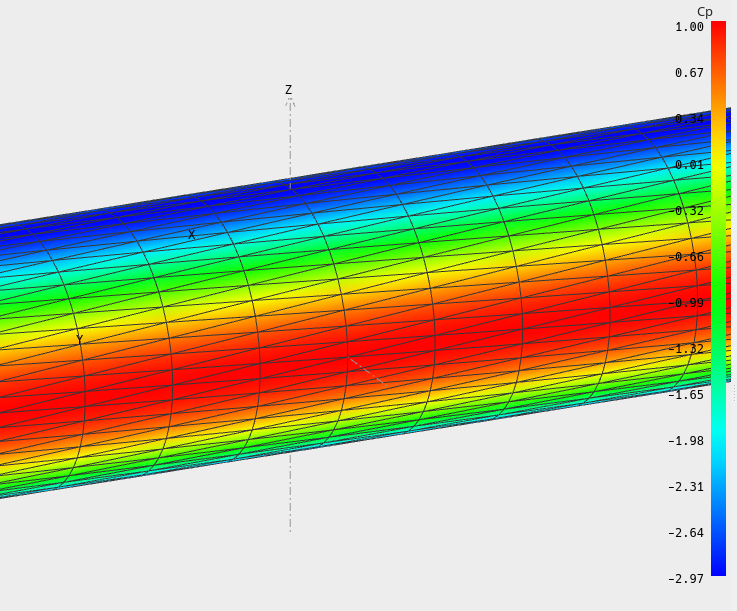
Cylinder

The pressure coefficient on the surface of a cylinder is Cp = 2 cos(2θ)-1
where the origin of the angle θ is taken at the leading point.
The pressure coefficients are therefore:

Cp=1 at the leading point.
Cp=-3 at the top point.

Back to top

Conclusion and recommendations

• All three methods give good precision for mesh sizes greater than 1000 elements.
• The linear triangular order method converges faster and is slighty more precise in the case of the sphere.
• The uniform triangular method is slightly more precise in the case of the cylinder.
• The use of the linear method does not seem to be justified with regard to its added complexity and the longer analysis times vs. the low benefit in Cp precision.

Project file: shapes.fl5

Back to top